백준 13325 - 이진 트리

www.acmicpc.net/problem/13325

13325번: 이진 트리

이 문제는 이진트리를 다루는 방법을 익히기에 좋은 문제라고 생각한다. 이진트리에서는 하나의 노드가 단 2개의 자식 노드만 가질 수 있다. 보통

1. 자식노드들에서 부모 노드로 올라올 때 어떠한 처리를 통해서 2개의 자식 노드가 가지는 값들을 합치거나, 나누거나, 평균값을 구하거나 등의 처리를 하는 경우가 있고, 

2. 반대로 부모노드에서 자식 노드로 내려갈 때, 어떠한 처리를 통해 나눠주거나 하는 메커니즘이다.

 

이 문제에서는 정점과 정점 사이에 있는 간선에 가중치가 부여되어있다고 하지만, 그 가중치를 그냥 정점에 기입하여 표현하였다.

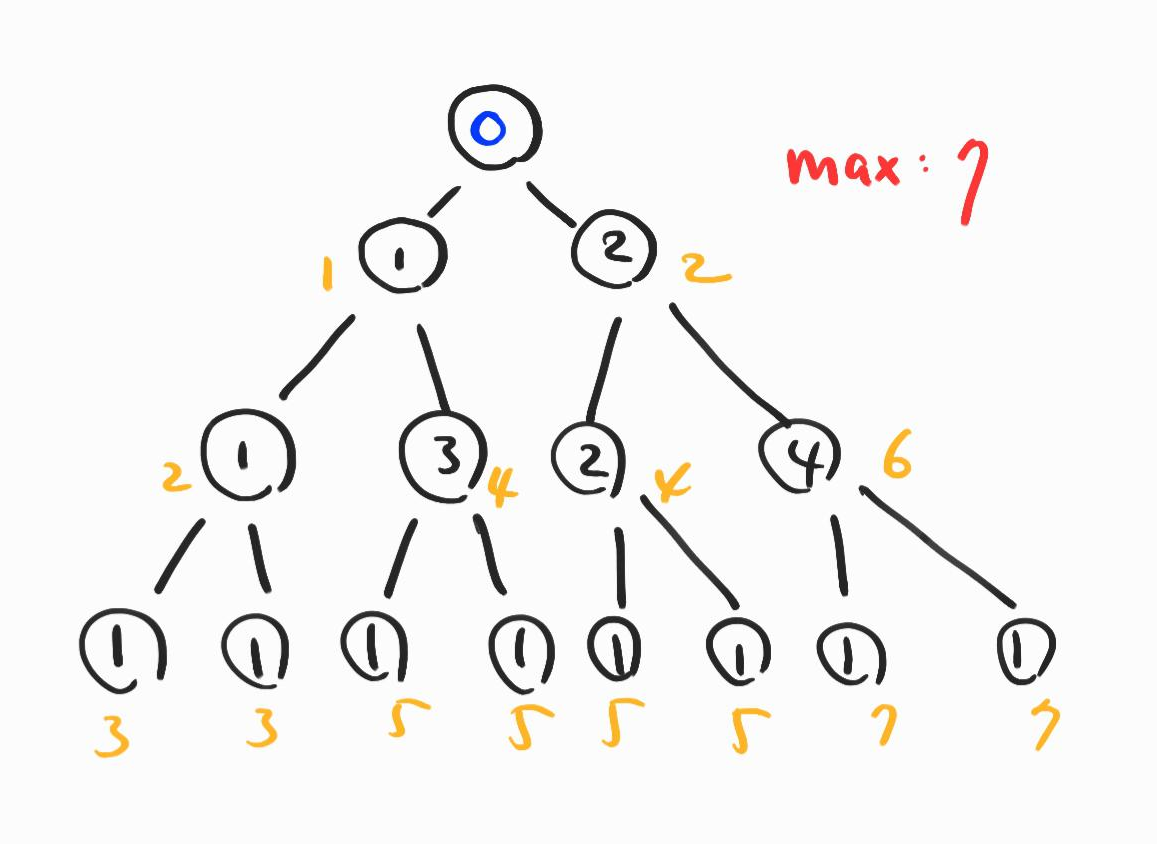
위의 그림은 문제에 있는 예제3번을 형상화하였다. 루트 노드(최상위 노드)에서 0으로 시작하여 각 정점을 거치며, 값을 누적해 나간다. 그러면 리프 노드(말단 노드)에서 누적값들이 계산되는데 여기서 7이 가장 큰 값임을 확인할 수 있다. 가중치 증가를 최소화하여야 하므로, 당연히 누적값이 최대인 경로상의 가중치는 증가시키지 않는다. 

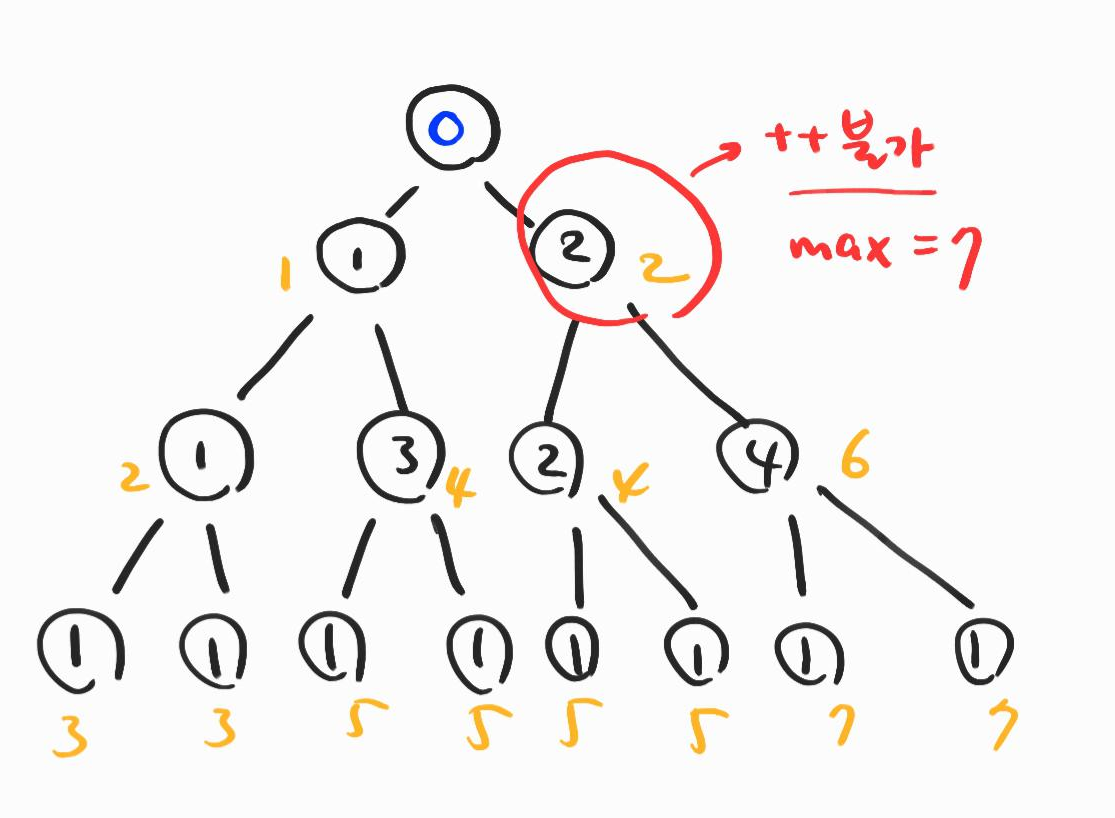
위의 그림과 같이 루트의 오른쪽 자식 노드는 최대값을 가지는 경로상의 노드이므로 가중치를 증가시키지 않고 다음으로 넘어간다.

그다음 깊이로 내려가면 오른쪽 4는 더 이상 증가시킬 수 없지만, 왼쪽에 있는 2는 증가시킬 수 있다. 최대값인 7에 미치지 못하기 때문이다.

 

이쯤 되면 대단히 중요한 사실을 한 가지 눈치챌 수 있는데, 그것은 바로 위의 그림에 기입하였듯이,

항상 낮은 깊이의 노드를 잇는 가중치를 증가시켜야 총 증가량을 최소화할 수 있다는 점이다.

아래에서 +1, +1을 해야 할 때, 부모노드에서 +1해 주면 자식 노드들은 +1을 할 필요가 없으니 그만큼 증가량을 절약할 수 있다. 그러므로 항상 루트노드에서 리프 노드를 향해 내려가면서 가중치를 증가시키는 방식으로 문제를 해결해야 한다.

 

아래 그림과 같이, 2였던 값을 4로 증가시키면 해당 경로는 7을 갖게 된다. 그리고 자식 노드로 향하는 가중치는 증가시키지 않아도 된다.

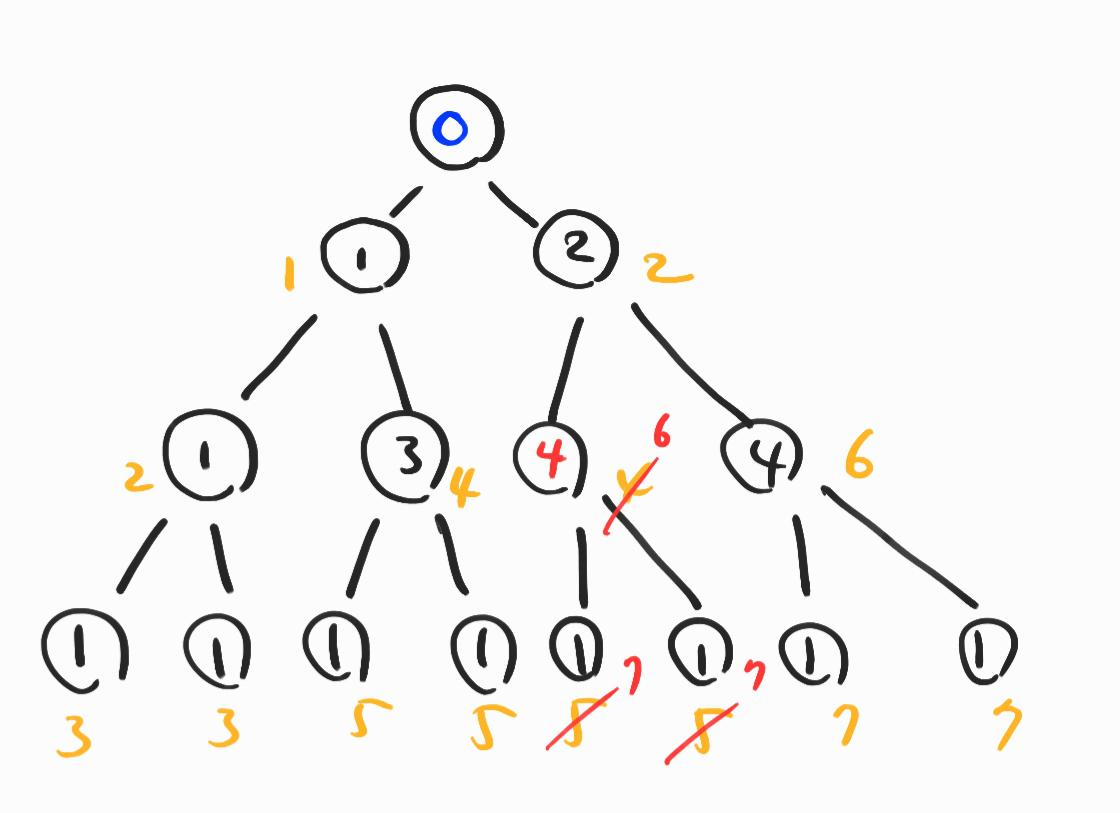
필자는 트리를 나타내는 배열 2개를 사용하였는데, 하나는 기존 정점의 값을 기입하였고, 다른 하나는 가중치의 누적값을 기록하였다.

주황색으로 표시된 값들이 누적값이 된다. 리프 노드에서 시작하여 부모 노드로 올라가면서, 부모 노드에서 자식들 중 max를 취한다. 그리고 자기 자신과 더하여 누적값을 기록한다. 즉, 위의 그림에서 3이 기입된 노드는 7이라는 값이 기록된다. 이런 식으로 리프에서 루트까지 올라가면서 가중치를 누적해두면, 루트에서 리프로 내려올 때, 해당 정점에서 얼마만큼 가중치를 증가시킬 수 있는지를 알 수 있게 된다.

 

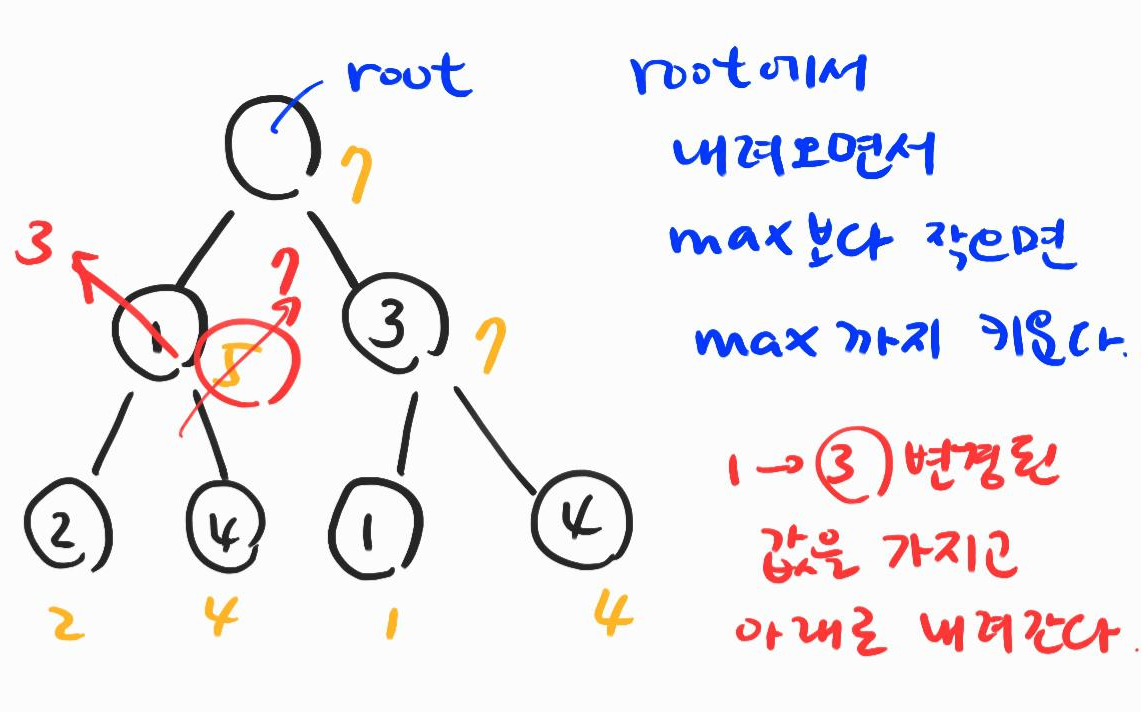
위의 그림과 같이 루트에서 내려오면서, 루트의 왼쪽 자식노드에서는 누적값이 5이므로 2만큼 (최댓값 7-현재 값 5=2) 증가시킬 수 있다. 그리하여 1+2=3이 되고, 아래로 내려갈 때 이 3을 갖고 내려간다.

 

위에서 내려온 3과 현재값 2의 합은 5이므로 아직도 7보다 작다. 고로 현 정점에서 2만큼 더 증가시켜야 한다.

위의 부모노드에서 3까지밖에 증가할 수 없던 이유는 그 노드의 오른쪽 자식 노드가 4를 갖고 있으므로 더 이상 증가시키면 최대값 7을 초과하게 되기 때문이다. 그래서 리프 노드에서 부모로 올라올 때, 부모 노드는 자식들 중 최대값을 취하는 것이다.

 

위와 같은 방법으로, 문제를 풀이할 수 있다. 필자는 누적값을 기록하거나 탐색하는 방식에 세그먼트 트리를 순회하는 방식을 그대로 적용하였다. 세그먼트 트리에 대한 것은 추후에 따로 포스팅하도록 하겠다. 매우 강력하고 어렵지 않은 자료구조이기 때문이다.

 

<주요 내용>

이진트리, 트리순회, 트리DP, 세그먼트 트리

 

<코드>

세그먼트 트리는 그저 필자가 사용한 방법이고, 이 문제를 세그먼트 트리라고 분류하기엔 무리가 있다. 그 점 참고 부탁드린다.

#include <iostream>
#define endl '\n'
using namespace std;
const int sz=1<<21;
int s,n,tree1[sz],tree2[sz];
// d = inheritance
void travel(int i,int d){
    if(d+tree2[i]<tree2[1])tree1[i]+=tree2[1]-(d+tree2[i]);
    s+=tree1[i];
    if(i<(1<<n)){
        travel(i<<1,tree1[i]+d);
        travel(i<<1|1,tree1[i]+d);
    }
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(NULL);cout.tie(NULL);

    cin>>n;
    for(int i=2;i<(1<<(n+1));++i)cin>>tree1[i];
    for(int i=(1<<n);i<(1<<(n+1));++i)tree2[i]=tree1[i];
    for(int i=(1<<n)-1;i>0;--i)tree2[i]=max(tree2[i<<1],tree2[i<<1|1])+tree1[i];
    // tree2[1]=max
    travel(1,0);
    cout<<s;
    return 0;
}