백준 1948 임계경로

www.acmicpc.net/problem/1948

1948번: 임계경로

이 문제는 위상정렬로 풀 수 있는데, 조금 더 생각할 부분이 있다. 최장거리는 구할 수 있지만, 최장거리를 만드는 경로의 개수를 세는 부분이다. 사실 최장거리를 구하기 위해 꼭 위상정렬을 할 필요는 없으나, 그 방법을 소개하고자 한다.

 

위상정렬을 모른다면 반드시 본 블로그내의 관련 포스팅을 참조하기 바란다. 위의 그림과 같이, 각 정점에 들어오는 간선의 개수 (indegree)를 정리할 수 있다. 1번도시는 들어오는 간선이 없으므로, 시작정점이 되고 위상정렬 결과의 선두에 있게 된다. order는 위상정렬된 결과를 보여준다. 즉 0부터 시작해서 연결된 다음 도시로 이동하면 되는 것이다.

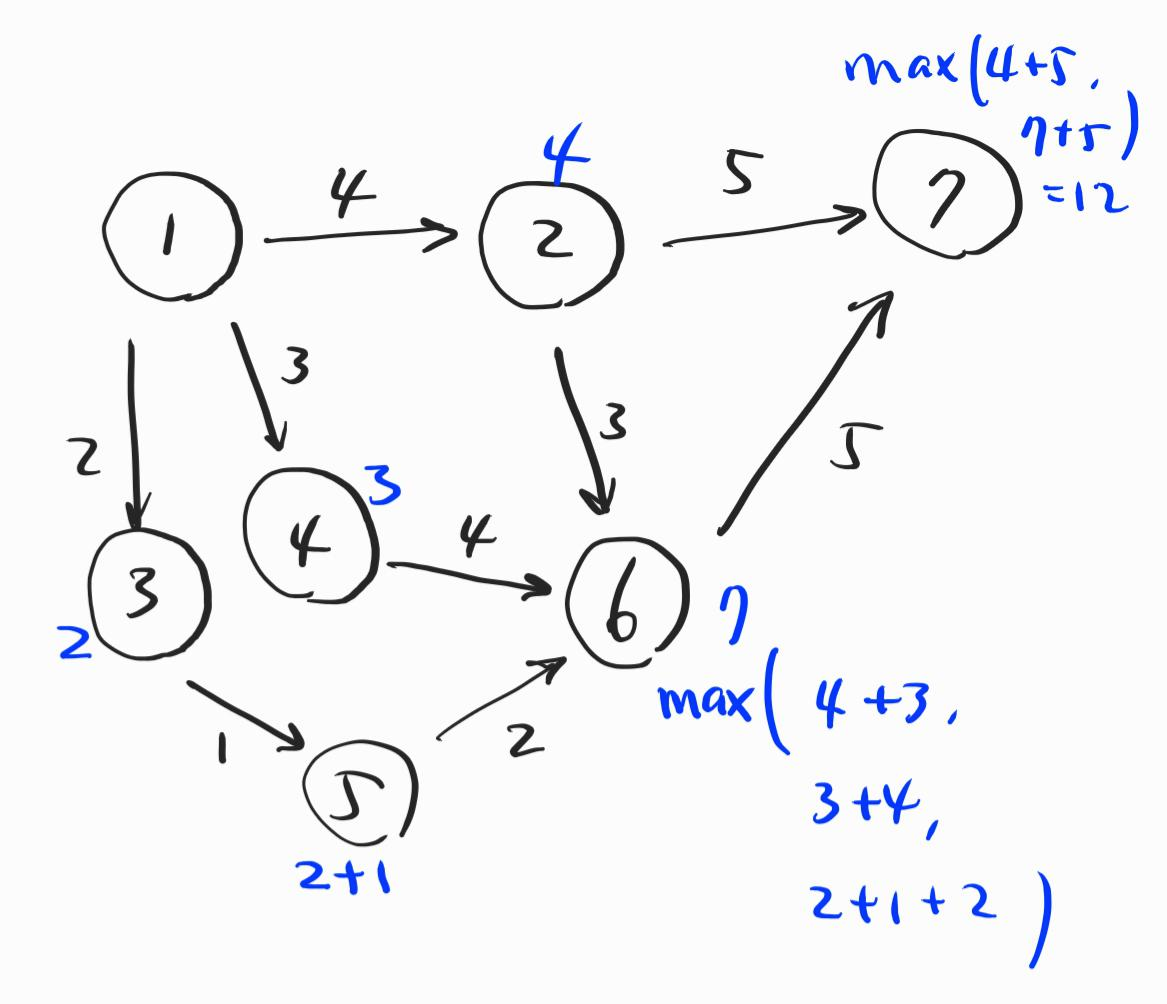
위의 그림과 같이, 위상정렬된 순서대로 방문하면서 각 도시에 모여지는 비용의 최대값을 취하여 기록해준다. 이런 식으로 끝까지 누적하면 최종 목적지 7번 도시에 12가 오게 되고, 이 값이 바로 최대 비용이 된다. 여기까지는 어렵지 않다.

 

이제 그 최대값12를 만드는 경로들의 개수를 세야 한다. 이 방법에 대해 고민해보면, 어떠한 간선을 지나 한 정점에 도달했을 때, 그 간선에서 소모한 비용 + 도달 정점에서의 최대 비용 = 총 최대 비용(12)이면 해당 간선이 바로 최대 비용을 만드는 간선임을 알 수 있게 된다.

그렇다면 시작점 1에서 0으로 시작하여 비용이 누적되어나가는데 중간 정점에 모이는 값들의 최대값을 어떻게 미리 알아둘 수 있을까?

필자가 생각한 방식은 목적지에서 거꾸로 오는 것이다. 같은 그래프 정보를 유지하면서 간선의 방향만 바꿔주는 것이다. 그렇게 하여 목표점에서 출발점으로 오면서 비용을 기록해두는 것이다. 위의 그림에서 2번 정점의 비용 값은 8이고, 4번 정점에 기록될 비용은 9인데, 이것이 뜻하는 바는 목적지 7번에서 시작하여 각 정점에 도달하는 방법 중 가장 멀리(오래) 돌아서 오는 길을 택했을 때 걸리는 비용이라는 뜻이다.

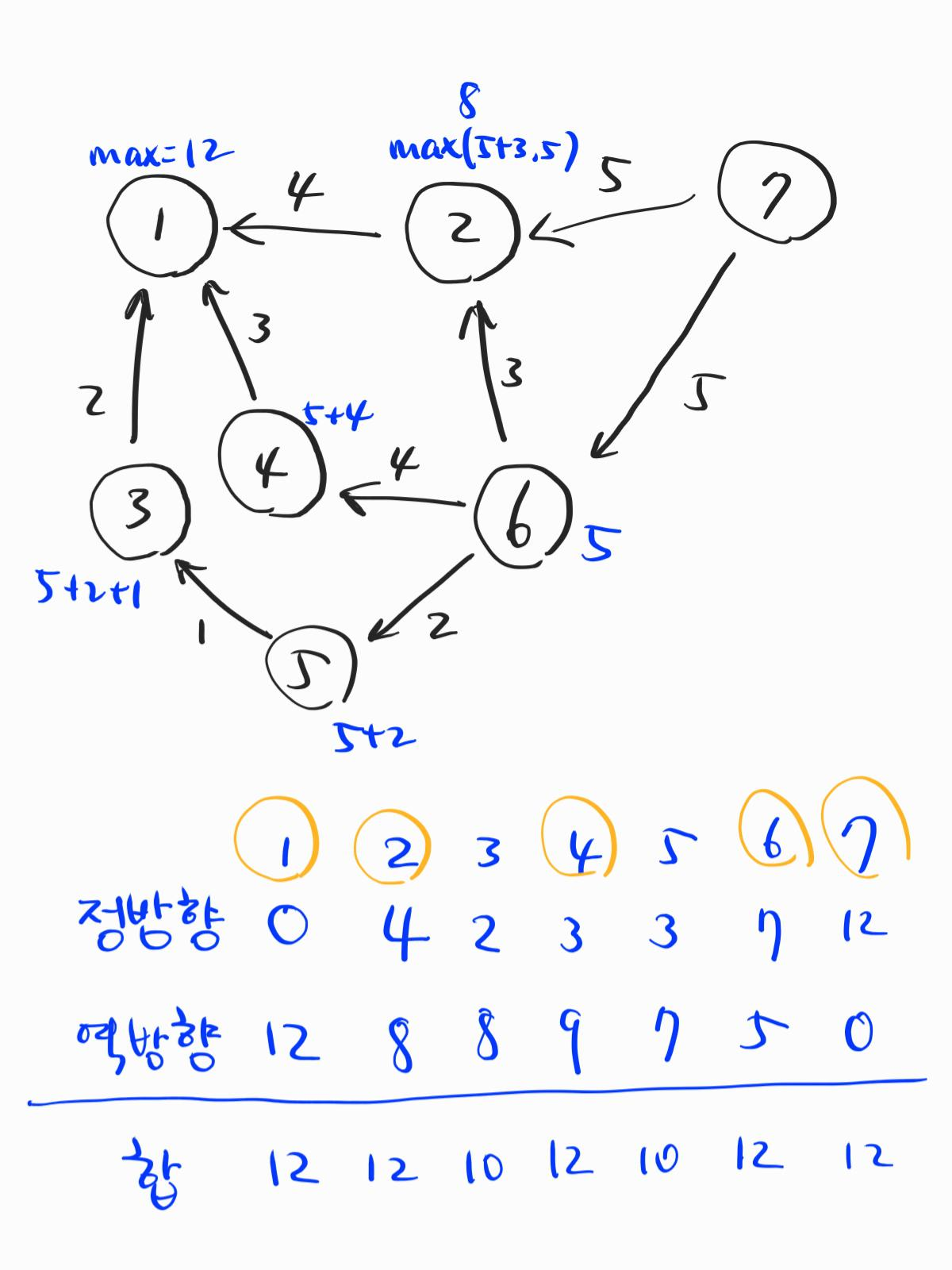
위의 그림과 같이, 표로 그려볼 수도 있겠다. 사실 이 문제를 풀기 위해선 역방향 비용만 정리해두면 된다. 표는 이해를 돕기 위해서 그려보았다. 합이 12가 되는 정점을 지나는 간선이 최대비용을 만드는 간선이 될 수 있다. 정점들 마다 합을 구해둔 것을 토대로 1,2,4,6,7을 연결하는 모든 간선이 전부 최대비용을 내는 간선이다라고 생각하는 것은 위험할 수 있다. 위의 표는 이해를 돕기 위해 정리한 것일 뿐이며, 실제 간선을 찾기 위해선 BFS 등을 통해서 탐색하며 합이 12가 나오는지를 체크하는 방식을 써야 한다.

 

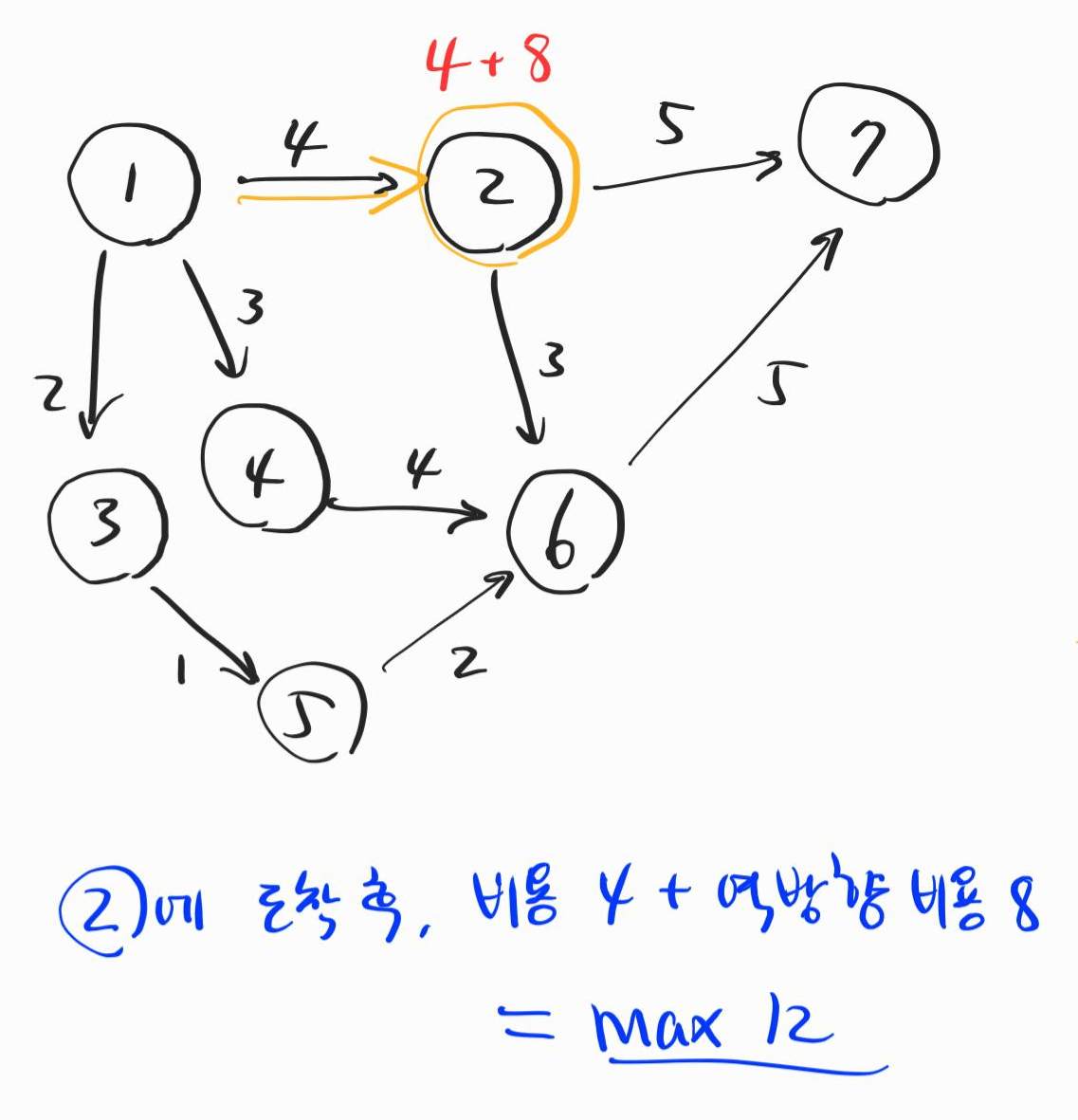
위와 같이 1에서 출발하여 2로 가면 비용이 4가 드는데, 역방향에서 왔을 때 비용은 8이었다. 두 수를 합한 것이 총 비용이다. 그 값이 미리 찾아둔 12와 같다면 1-2 간선은 쉬지 않고 달려야 하는 간선이 되는 것이다.

 

일반적인 그래프 탐색을 통해 값을 누적하여 나가다가 역방향에서 온 비용과 합산하여 12가 되는 모든 간선을 찾아주면 된다. 위의 그림이 쉬지 않고 가야 하는 간선들을 나타낸다.

 

<주요 내용>

위상정렬, 그래프 뒤집기, 역방향 간선

 

<코드>

첫 위상정렬 후 탐색을 통해 최대비용을 구하고,

역방향 그래프 탐색을 통해 각 정점별 비용을 기록해두고,

다시 정방향 그래프 탐색을 통해 최대 비용 간선을 찾았다.

#include <iostream>
#include <queue>
#include <vector>
#define endl '\n'
typedef long long ll;
using namespace std;
const int sz=1e4+1;
vector<pair<int,int> >graph[sz],graph_rev[sz];
queue<pair<int,bool> >q,q_rev;
queue<int>nq;
int indegree[sz],a,b,c,n,m,start,goal,qs,start_rev,goal_rev,cnt;
int indegree_rev[sz];
bool visited[sz];
ll cost[sz],cost_rev[sz];

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(NULL);cout.tie(NULL);

    cin>>n>>m;
    while(m--){
        cin>>a>>b>>c;
        graph[a].push_back(make_pair(b,c));
        indegree[b]++;
        graph_rev[b].push_back(make_pair(a,c));
        indegree_rev[a]++;
    }
    cin>>start>>goal;
    for(int i=1;i<=n;++i){
        if(!indegree[i]){
            if(i==start)q.push(make_pair(i,1));
            else q.push(make_pair(i,0));
        }
        if(!indegree_rev[i]){
            if(i==goal)q_rev.push(make_pair(i,1));
            else q_rev.push(make_pair(i,0));
        }
    }
    while(!q.empty()){
        auto currp=q.front();q.pop();
        auto curr=currp.first;
        for(auto nxp:graph[curr]){
            auto nx=nxp.first;
            if(currp.second){
                cost[nx]=max(cost[nx],cost[curr]+nxp.second);
            }
            // 도중에 start를 만났는데 목표정점에 아직 진입간선이 남아있는 상황에 주의!
            if(!--indegree[nx]){
            	q.push(make_pair(nx,(nx==start)|currp.second|cost[nx]));
            }
        }
    }
    cout<<cost[goal]<<endl;

    while(!q_rev.empty()){
        auto currp=q_rev.front();q_rev.pop();
        auto curr=currp.first;
        for(auto nxp:graph_rev[curr]){
            auto nx=nxp.first;
            if(currp.second){
                cost_rev[nx]=max(cost_rev[nx],cost_rev[curr]+nxp.second);
            }
            // 도중에 start를 만났는데 목표정점에 아직 진입간선이 남아있는 상황에 주의!
            if(!--indegree_rev[nx]){
            	q_rev.push(make_pair(nx,(nx==goal)|currp.second|cost_rev[nx]));
            }
        }
    }

    nq.push(start);
    while(!nq.empty()){
        auto curr=nq.front();nq.pop();
        for(auto nxp:graph[curr]){
            auto nx=nxp.first;
            if(cost[curr]+nxp.second+cost_rev[nx]==cost[goal])cnt++;
            if(!visited[nx]){
                visited[nx]=1;
                nq.push(nx);
            }
        }
    }
    cout<<cnt<<endl;
    return 0;
}