유니온 파인드는 익히기도 쉽고, 응용 범위도 넓어서 아주 좋아하는 편이다. 간단한 유파는 구현도 쉽고.
꼭 PS가 아니라도 프로그래밍을 하다 보면, 뭔가 동시적으로 (concurrently or simultaneously) 값을 바꾸는 등의 작업을 구현하고 싶을 때가 참 많다.
- 2가 1의 자식 노드인데, 1의 값을 변경함으로써 2도 어떠한 처리를 해주거나,
- 우선순위 큐에 이미 들어있는 값인데, 어떤 처리를 통해 그 안의 값이 바뀌면서 순서가 역전되거나,
- 복잡하게 얽힌 그래프 속에서 하나의 정점만 바꿔도 그 안에 연결된 모든 정점을 같이 바꾼다거나,...
그럴 때 마치 집합처럼 정점들을 엮어주고, 빠르게 처리를 해줄 수 있는 것이 바로 유니온 파인드이다.
유니온 파인드는 유니온 함수와 파인드 함수 2가지를 통해 구현한다. 그 중에 파인드 함수 내부는 root[n]=find(root[n])이다.
아래의 그림을 보자.

위의 그래프에서 예를 들어, 1이 인싸이고, 인싸가 있는 그룹 내에 있는 모든 친구들이 전부 인싸가 된다라고 한다면,
4번 친구의 경우, 3과 2를 거쳐 1까지 가야 자신이 인싸임이 확인된다. 이제 만약 정말 많은 친구들이 일렬로 늘어서 있다면 인싸 확인에 너무나 오랜 시간이 걸릴 것임이 자명하다. 그래서 위에서처럼 1-2-3-4로 연결된 그래프 안에서 하나의 수를 처리함으로써 다른 모든 값을 빠르게 바꾸기 위해서는 아래의 변경된 형태 (1이 루트, 나머지가 자식 노드)로 바꾸어야 한다. 또는 다른 정점이 루트에 있거나 하는 등으로.
그리고 그 처리를 해주는 것이 바로 유니온 파인드이다.

위의 그림을 보면 root라는 표현이 등장한다. 각 정점에 대해 루트가 무엇인지를 정해두어 그것을 통해 해당 정점이 어떠한 조건을 만족하는 지를 빠르게 판단할 수 있는 것이다.
처음에는 그 루트 배열의 어떤 약속된 초기값으로 초기화해둔다. 문제에 따라 다르겠지만, 0,1,-1 또는 자기 자신으로 만들어둔다. 초기 상태라 함은 아직 체크되지 않은 상태일 수도 있지만, 아랫줄에 있는 재귀 함수를 돌지 않기 위한 어떤 탈출 조건일 수도 있다. 그리고 아직 초기 상태라면 그 값 자체를 리턴해도 되지만, 또는 어떤 약속된 기본값을 리턴하도록 설정할 수 있다. 즉, 초기값=기본값일 수도 있고, 다를 수도 있다. 그런 부분들은 모두 문제에 따라 유동적으로 적용해야 하는 부분이다.
그리고 초기 상태가 아니라면 파란 네모로 표시된 root[n]=find(root[n])을 수행하게 되는데, 이 부분이 바로 본 유니온 파인드의 핵심적인 부분이다.
재귀적으로 find함수를 계속 불러서 자기 자신의 루트를 인싸와 직접 연결해주는 역할을 한다.
매번 재귀로 N번을 파고 들어서 인싸를 찾는다고 생각할 수 있지만, 한번 인싸와 연결되면 이제 if root[n]==초기값(또는 인싸)에서 필터링이 되어 바로 리턴되기 때문에, 다시 그 모든 과정을 반복하지 않는다.
이제 아래의 유니온 함수를 살펴보자.
def union(a,b):
# a와 b중 어떤 조건을 만족하는 수가 다른 수의 자식 노드가 된다.
# 여기서 중요한 점은 a와 b를 직접 연결하는 게 아니라 그들 그룹의 장을 연결시켜야 한다는 점이다.
rootOfA=find(a)
rootOfB=find(b)
root[rootOfA]=rootOfB유니온 함수는 2개의 정점을 받아 (몇 개의 정점을 받는지도 모두 사용자가 유동적으로 조절할 수 있을 것이다) 인싸가 있다면 인싸가 아닌 정점의 루트를 인싸로 연결해주는 것이다. 이런 식으로 정점들을 연결하면 이후에 find함수를 통해 해당 정점의 루트가 누구인지를 추적할 수 있게 되는 것이다.
즉, 이제 가장 최상단 루트값들의 서열만 정리하면(?), 다른 모든 값들은 root[n]을 구했을 때, 조건을 만족하지 않기에 재귀를 통해서 새로운 루트로 업데이트되게 되는 것이다. 그렇다고 루트값이 바뀌었다고 모든 관련된 정점들이 전부 업데이트 된다면 또 다른 문제가 있을 수 있다. find를 통해 해당 정점의 루트가 누구인지 찾을 때만 업데이트된다. 즉, 어떠한 정점의 루트가 누구인지를 알고 싶다면 root[n]을 통해 접근하는 것이 아니라 find함수를 통해 찾아야 한다. 약간 lazy 같은 느낌도 있다. 아래의 그림을 보자.
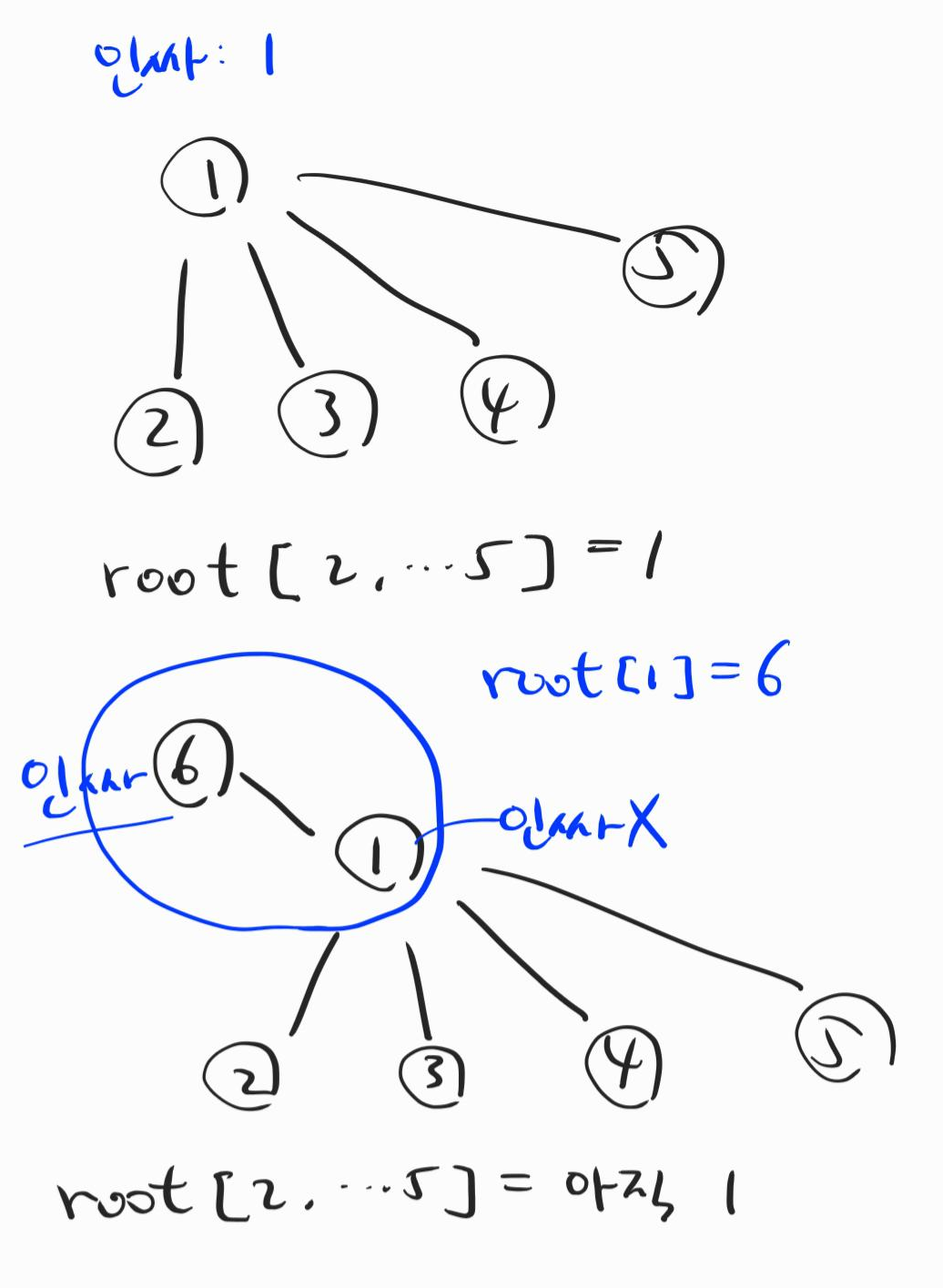
1이 인싸이고, 2,3,4,5가 1에 묶여있는 형태이다. 이때 물론 2부터 5번 친구들의 루트는 1이다. 근데 만약에 이제 1은 인싸가 아니고 6이 인싸라고 한다면 위의 그림에서 아래쪽처럼 변경된 형태(6이 1의 부모 노드가 되어있는 형태)가 된다.
하지만 루트값이 업데이트되었다고 (root[1]=6) 2,3,4,5가 즉각적으로 바뀌진 않는다. 그래서 2부터 5까지의 루트는 아직 1인 상태이다.
이제 아래의 그림을 보자

find(2)를 했다고 가정하면, root[2]=1인데 1이 이제 인싸가 아니므로 재귀함수를 시작하게 된다. find(root[2])를 수행하게 되고, 즉 find(1)이 되어 6이 리턴된다. 6은 인싸라서 find(1) 함수 안에서 재귀를 돌지 않고 바로 나올 수 있는 것이다. 이제서야 root[2]는 6으로 업데이트되었다. 아직도 3번부터 5번까지의 루트는 1이다.
지금까지의 내용을 다시 정리해보면 아래와 같다.
- 루트를 탐색하는 과정에서 재귀를 돌더라도 한번 업데이트된 값은 빠르게 재귀를 탈출한다는 점
- 루트가 업데이트되더라도 다른 관련 정점들은 find함수를 통해야 업데이트된다는 점 (일괄적으로 즉시 업데이트되는 것은 아님)
- 그래서 어떤 정점의 루트를 찾고자 하면 반드시 find함수를 통해야 한다는 점
- 유니온 함수를 통해 묶어줄 때 문제의 조건을 만족하는 정점이 루트가 되도록 해야 한다는 점
필자는 개인적으로 find함수가 매우 중요하다고 생각한다. 유니온 함수는 문제에 여러 가지 방식으로 변형될 수 있고, 심지어 없어도 된다!
그리고 시간복잡도를 구함에 있어 amortized라는 표현이 등장하는데, 유니온 파인드의 시간복잡도 증명은 상당히 어려운 것으로 알고 있다. 한 가지 확실한 것은 시간 세이브를 크게 할 수 있다는 것이다.
유니온 파인드에서 union 으로 연결된 정점들은 일종의 그룹을 만들게 된다. 자연히 그들은 대표를 갖는다. 그리고 그 대표 정점의 식별자가 해당 그룹의 식별자이기도 하다.
- 한 정점이 어떤 그룹에 포함되는지
- 어떤 정점과 다른 정점이 같은 그룹에 있는지 (연결되어 있는지)
- 각 그룹에는 몇 개의 정점이 포함되는지
- 총 몇개의 그룹이 있는지
- 어떠한 그룹에도 포함되지 않은 독립된 정점이 있는지, 몇 개 있고 그들이 누구인지.
위와 같은 다양한 정보를 얻을 수 있다.
아래의 연습 문제를 통해 더욱 이해도를 높여보자
<연습 문제>

