백준 2098 외판원 순회

https://www.acmicpc.net/problem/2098

2098번: 외판원 순회

대단히 중요한 문제 중 하나라고 생각한다. 비트마스킹 + 재귀 + DP 가 어우러진 좋은 문제이다. 문제에서도 "computer science 분야에서 가장 중요하게 취급되는 문제"라고 언급하고 있다.

 

이 문제를 해결함에 있어 깨달아야 하는 몇가지 중요한 점 중 하나는 여행을 어디에서 시작해도 상관없다는 점이다. 왜냐하면 항상 시작한 도시로 돌아와야 하기 때문이다. 다른 문제 중에 백준 1185 유럽여행 같은 경우는 N-1개의 경로만 남겨야 하지만, 이 문제에서는 모든 경로를 사용할 수 있으므로, 사이클의 형태가 만들어지게 된다. 

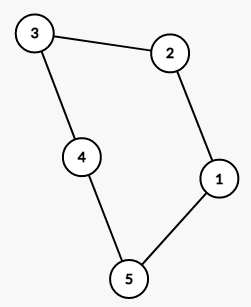
1에서 시작하여 1-2-3-4-5-1 의 사이클이 왕복 여행을 완료하는 가장 최단 경로라고 하자. 모양은 오른쪽과 같이 만들어진다. 

여기서 3에서 시작하든, 5에서 시작하든 어디서 시작해도 완성된 형태는 왼쪽처럼 나타나게 된다.

 

문제에서 주어지는 도시의 갯수가 총 몇 개인지 알 수 없으므로, 항상 1번에서 시작하면 되겠다.

 

 

 

 

 

 

또 다른 중요한 점은, 문제에서 N은 16밖에 안된다. 그도 그럴 것이, 모든 경로를 다 따져봐야 하므로 이 값이 크면 너무 많은 경우의 수를 체크해야 하게 된다. 근데 여기서 중요한 힌트를 얻을 수도 있다. 사실 이 부분은 알고리즘 문제들에서 보이는 큰 힌트이기도 하다. N이 작으니, 비트마스킹 사용 가능성이 생기는 것이다; (물론, 이런 식으로 생각해서는 안된다...)

 

정답부터 말한다면,

보통 집에 하나씩 갖고 있는 데이터 저장용 2차원 배열, dp[i][mask]를 준비한다.

i는 도시의 번호가 되고, mask는 현재 상태가 된다. 비트마스킹을 사용하기에 mask라고 이름 지었다.

여기서 정의해야 할 부분은 dp[i][mask]는 'i번째 도시에 mask의 상태로 진입했을 때 여행 완료를 위해 발생하는 여러 총 비용 중 최솟값'이라는 것이다. 

 

1. 1번 도시에 진입한다. 물론 mask는 1이다 00001(2진수) = 1이므로.
2. 각 도시에서 연결되는 다음 도시를 탐색한다. 여기서 케이스가 나뉜다.
3. mask가 (1<<n)-1 의 상태가 되면 1번 도시로 돌아가는 비용을 리턴한다. (1<<n)-1은 111111(2)로써 모든 도시를 방문한 상태이다.
4. 여러 케이스의 비용 중 최솟값을 dp에 저장하고 그 값을 리턴한다.
5. 후에 같은 도시에 같은 상태(같은 마스크)로 진입 시 이미 구해둔 값을 바로 리턴한다(여기서 시간복잡도를 크게 낮춘다)

위와 같은 방법으로 문제를 해결한다.

예를 들어, 1, 2, 3을 방문한 상태로 4에 진입했을 때,

1 - 2 - 3 - 4 였을 수도 있고,

1 - 3 - 2 - 4 였을 수도 있다.

두 가지 케이스가 사실 같은 상태로 4번 도시에 진입한 것이다. 만약 아직 방문할 도시가 12개나 남았다면, 많은 계산이 중복으로 이루어진다. 하지만 4번 도시에서 해당 상태의 최소 비용을 미리 저장해둠으로써, 중복 계산을 피할 수 있다.

 

 

위는 정답이었고, 오답이 발생할 수 있는 케이스를 생각해보자. 위에는 고심 후 발견한 방법을 정리했기에 쉽지만, 항상 처음에 저러한 풀이를 구축(?)할 때는 많은 생각이 필요하다.

만약 cost 값을 매번 다음 재귀로 넘겨준다면 어떻게 될까?

문제를 해결하는 함수명이 tsp라고 하자. 해당 함수에서 다시 재귀 호출할 때, 인자로 현재의 cost와 다음 도시로 가는 비용을 더한 값을 넘겨주는 것이다. 그래서 매번 최솟값만 저장해주면, 결국 답이 나오는 것 아닌가라고 생각했다.

# 오답코드임!

def tsp(s, mask, cost):
    global n
    if dp[s][mask] != -1:return dp[s][mask]
    if mask == (1 << n)-1:return cost+w[s][0] if w[s][0] else big

    dp[s][mask] = big

    for nx in range(n):
        if not w[s][nx]:continue
        if (1 << nx) & mask:continue

        dp[s][mask] = min(dp[s][mask], tsp(nx, (1 << nx) | mask, cost+w[s][nx]))

    return dp[s][mask]

이렇게 하면 tsp 1차에서 호출한 tsp 2차가 리턴하는 값은 항상 최소 비용이므로 그걸 현재의 tsp 1차에 바로 넣어주면 된다고 생각했다.

하지만 이 경우에는 중대한 문제가 있다. 함수 내의 초반부에 dp[s][mask]!=-1 인 경우, 바로 리턴을 할 수 없게 된다. 지금까지 쌓아온 cost값이 최솟값이라는 보장이 안되기 때문이다. 그저 사이클을 한 번만 완성하면 dp에 저장되고 이후에는 그 값이 최솟값이라고 믿게 된다. 그렇다고 그 분기점에서 다시 한번 최솟값인지를 체크한다면 로직도 지저분해지게 된다.

 

<알고리즘>

재귀, DP, 비트마스킹

 

<코드>

import sys
si = sys.stdin.readline

n, w, big = int(si()), [], 16*int(1e6)+1
dp = [[-1 for _ in range(1 << n)]for _ in range(n)]
for _ in range(n):w.append([int(e) for e in si().split()])


def tsp(s, mask):
    global n
    if dp[s][mask] != -1:return dp[s][mask]
    if mask == (1 << n)-1:return w[s][0] if w[s][0] else big

    dp[s][mask] = big
    for nx in range(n):
        if not w[s][nx] or (1 << nx) & mask:continue
        dp[s][mask] = min(dp[s][mask], w[s][nx]+tsp(nx, (1 << nx) | mask))
    return dp[s][mask]

print(tsp(0, 1))

위처럼 매 지점에서 왕복을 마칠 때까지의 값만을 따져야 한다. 그래야 지금까지 온 경로와 상관없이, 이후 경로들의 비용 합 중 최소값을 온전히 구하고, 그 윗 단계에서 다시 최소 비용을 따질 수 있게 된다! 

첫 도시에서 분기, 그 다음 도시에서 또 분기되므로, 아래 단계에서부터 최솟값을 확정해서 올라가야 한다는 것이다.