비교적 빠른 습득이 가능하고, 효용성도 좋은 알고리즘이라고 생각한다.
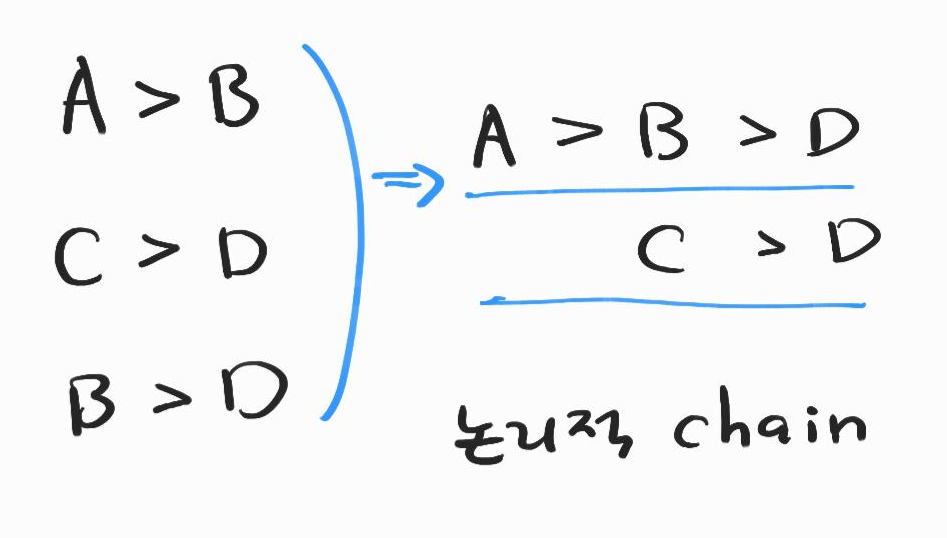
문제를 보면 위의 그림과 같이, A,B,C,D가 만드는 쌍(pair)에 대한 관계를 표현하고, 이를 통해 일종의 논리적 체인을 구성해야 하는 일이 있다. 그리고 아래와 같이, 그래프 상에서 DP를 해야하는 경우도 있다.

위의 그림을 조금 더 살펴보자.

위에서 처럼 A에 1을 놓고 전파를 시작한다. A에서 갈 수 있는 정점은 B와 C이므로 B와 C에 A로부터 받은 1을 합산해준다.(모든 정점의 초기값은 0이었다, A를 제외하고.)

위와 같이, E까지 전파하면, BFS를 돌렸을 때, 모든 정점에 대한 방문체크가 끝나고, 그림에서와 같은 값을 갖게 된다. 하지만 이는 올바르지 않다. 전파하는 와중에 값이 변경된 정점이 있기 때문이다.

C의 경우에, 자식노드 D와 E에 값을 전파함과 동시에 자신의 값도 1에서 2로 증가되었다. 하지만 D와 E에게 전파한 값은 1이다.

이런 문제를 해결하기 위해서는 어떤 정점에 대해, 자신에게 들어오는 모든 간선을 먼저 처리하고 나서, 자신의 자식노드로 넘어가야 한다. 즉, 정점 C는 자신에게 들어오는 간선이 2개 있고, B에서 오는 값이 들어오기 전에는 D와 E로 내려가면 안되는 것이다. 즉 정점들간에 출발 순서를 정해주어야 한다. 물론 들어오는 간선이 없는 정점이 가장 일찍 출발하게 될 것이다.

그 순서를 정함에 있어, 링크드리스트를 떠올리는 경우가 있을 수도 있다. 위와 같이, A->C, A->B, B->C 이므로 A->B->C가 성립한다. 그렇다면 그래프 정보를 입력 받을 때, A->C인 간선을 먼저 받았다고 한다면, 일단 둘을 연결해두었다가 B정보를 받은 후에 적절히 끊어주고 다시 연결하는 식으로 해야할까? 구현이 어렵고 불필요한 시간을 소모하게 된다. 이러한 문제를 해결함에 있어 아주 좋은 방법이 바로 위상정렬을 사용하는 것이다.
필자는 위상정렬은 '비선형 자료구조의 선형화'를 일으킨다고 생각한다.
이제 본격적으로 위상정렬을 어떻게 행하는지 알아보겠다. 위에서 만든 예제를 아래 그림에서 다시 살펴보자.

각 정점별로 들어오는 간선의 갯수를 기록하였다. 위상정렬을 구현하기 위해서는 Queue (또는 FIFO가 가능한 자료구조)가 필요하다. 그러므로 in=0인 A부터 큐에 담는다.

in=0인 정점을 모드 큐에 담은 후에 큐에서 앞에서부터 순서대로 하나씩 pop하면서 연결된 이웃정점의 in값을 하나씩 줄여주면 된다. 그리고 줄어들어 in값이 0이 되는 정점을 큐에 담아주면 되는것이다. 그리고 큐에서 pop된 순서대로 order벡터(또는 리스트)등에 담아주면 되는데 이 order가 바로 위상정렬된 결과가 된다!

같은 방식으로 계속 진행한다. 이제 C도 in=0이므로 큐에 들어온다. 그리고 pop된 B는 A의 뒤에 자리하게 된다. 이런식으로 끝까지 진행하면, 위상정렬의 결과는 [A B C D E]가 된다.
이제 이를 활용하여 문제를 해결할 수 있다. 처음에 A에 1을 넣고 시작한다 (dp['A']=1 또는 dp[0]=1 등으로 표현)


위상정렬된 순서대로 나아가면서 연결된 정점에 자신의 값을 물려준다. A를 봤을 때, B와 C에 각각 1이 들어가고, B를 본 후에, C는 1+1=2가 되고 D는 1이 된다.

이와 같은 방법으로 끝까지 진행하면 목적지인 E에 최종적으로 5가 들어감을 알 수 있다. 총 5가지의 경로가 있다는 뜻이 된다.
- A-B-D-E
- A-B-C-D-E
- A-B-C-E
- A-C-D-E
- A-C-E
위와 같이 위상정렬 (비선형 자료구조를 통해 선형화)를 통해 문제를 해결할 수 있다.
그리고 위상정렬에는 제한도 있고 또 다른 강력한 기능도 있는데,
제한은 기본적으로는 DAG(Directed Acyclic Graph, 사이클이 없는 단방향 그래프)에서만 사용가능하다는 점이다.
다른 기능은 DG(Directed Graph, 사이클이 있을 수 있는 단방향 그래프)에서 사이클의 존재여부를 찾을 수 있다는 점이다!
아래의 그림을 보자

1-2-3-4-5-1로 순환구조를 만들고 있다. 이럴 때는 위상정렬을 하기 위한 큐에 무엇이 들어갈 수 있을까?

위와 같은 예시도 보면, 1번은 in=0이므로 (들어오는 간선이 없음) 큐에 처음에 들어간다. 큐에서 1이 나오면서 2의 in값이 0이되고, 2도 큐에 들어간다. 하지만 그후에 더 이상 in=0이 되는 정점이 없다.
즉, 위상정렬을 하기 위한 처리가 끝난 후에 (queue가 비워지면 끝남), order상에 들어오지 않은 정점들은 사이클에 관여하는 정점들이라는 뜻이다! (하지만 큐에 들어오지 않는, 그러므로 order벡터에도 들어오지 않는 점들이 하나의 사이클을 구성한다는 뜻은 아니다) 그리고 단순히 사이클의 유무만 확인하고자 할 때는, order벡터의 길이와 전체 정점 수를 비교하면 된다. 같지 않으면 사이클이 있다는 뜻이 된다.
아래의 연습문제와 함께 포스팅을 마무리하겠다.
<연습문제>
본 포스팅은 알고리즘의 대가이신 류호석님의 도움을 받았음을 밝힌다. 그리고 그 분의 유튜브 동영상 강의도 첨부하겠다.
www.youtube.com/watch?v=HxHISRelNuM&t=360s



